En physique, il est souvent nécessaire de manipuler des relations de proportionnalité, comme celle, très souvent utilisée en mathématiques, qui relie la distance « d », la vitesse « v » et le temps « t » (durée) :
d = v . t
Le point remplaçant le signe « multiplier », cette relation peut également s’écrire : d = v x t
Il s’agit d’être capable, à partir de cette relation, d’écrire les deux suivantes :
v = d / t
t = d / v
Malheureusement, ces transformations sont sources de nombreuses erreurs, surtout lorsqu’il s’agit de travailler sur des relations de proportionnalités appliquées à la physique, comme par exemple :
U = R . I
E = P . t
P = U . I
Voici une méthode qui permet de limiter les erreurs.
Dans l’exemple qui suit, on utilisera la relation : d = v . t
1ère étape : on commence par dessiner un « T » majuscule
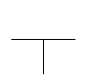
2ème étape : on écrit la relation, en prenant soin d’écrire LES DEUX TERMES qui sont MULTIPLIES (v et t) EN DESSOUS
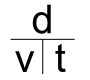
3ème étape : si on veut une relation exprimant « v » en fonction de « d » et « t », il suffit de noter que « d » est AU DESSUS de « t ».

« d » va donc se retrouver au dessus du trait de fraction :
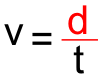
La relation exprimant « v » en fonction de « d » et « t » s’écrit donc :
v = d / t
De la même façon, la relation exprimant « t » en fonction de « d » et « v » s’écrit :
t = d / v
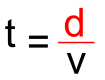
Application à des relations de proportionnalité utilisées en physique
Application 1 : relation U = R . I

C’est « U » qui se trouve « au dessus » du trait de fraction

On peut donc en déduire les deux relations suivantes :
R = U / I
I = U / R
Application 2 : relation E = P . t

C’est « E » qui se trouve « au dessus » du trait de fraction

On peut donc en déduire les deux relations suivantes :
P = E / t
t = E / P
Application 3 : relation P = U . I
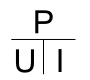
C’est « P » qui se trouve « au dessus » du trait de fraction :

On peut donc en déduire les deux relations suivantes :
U = P / I
I = P / U

www.objectif-s.fr – Soutien scolaire en physique-chimie de la 5e à la 2nde